Skip to content

把解决疫情问题模拟成ROI收益曲线

Simulating a Fight against Pandemic as a ROI model

by Hong Wu｜克林 @hongwuxyz

TL;DR

TL;DR by ChatGPT🤖

The global pandemic can be modeled as a function of two variables: the initial number of cases (n₀) and the basic reproduction number (R₀). Solving for n₀ yields a linear return, while solving for R₀ yields an exponential return. In other words, identifying and isolating initial cases can help slow the spread of the disease, while measures such as vaccination can help reduce the reproduction rate of the virus. This simplified model provides a framework for thinking about the pandemic and potential solutions to it.

太长；懒得读⏳

解决疫情其实是就是通过公共医疗手段减慢 n 的增长速度的赛跑。 \(n\): 是在某个时间t的最终阳性病例数。

  1. \(n\) 的增速不断增加，就代表增加阳性的人数比增加的阴性人数快，也就是“病人总量会越来越多”。
  2. \(n\) 的增速不断减少，就代表增加阳性的人数比增加的阴性人数慢，也就是“病人总量会越来越少”。
  3. \(n\) 的增速等于零的时候，就代表增加阳性的人数不再增加，那么随着阴性人数的增加，“病人总量会越来越少”。

由此我们可以把 \(n\) 模拟成一个由:
- 初始病例数n₀
- 基本传染数R₀

的函数：

\[f(n_0, R_{0}) = n\]

同时 \(n \propto 正比于 R_0\)， 通过模拟解决疫情的收益，我们可以得出：
解决 n 是线性回报， 而解决 和 R₀ 是指数型回报。
点击这里跳转到底部解读ROI曲线。

img

Exponetial Curve from Washington Post Source:Reference [1]

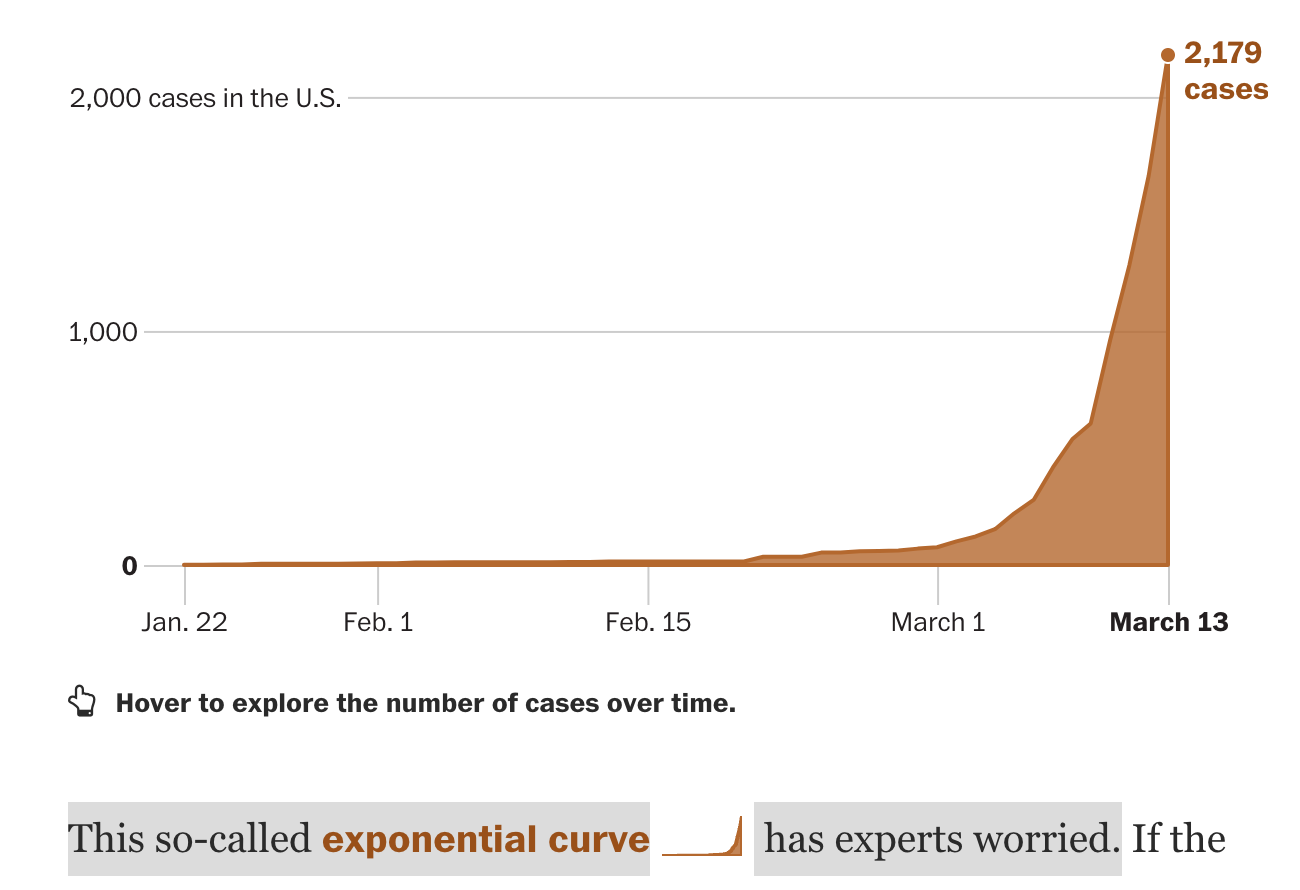
免责声明🙅🏻‍♂️

TL;DR 中的模型是非常宏观，非常 naive~朴素简化的，这篇短文更多是为大家提供一个基于少量量化模拟的定性分析。

更通俗的讲，你可以把这个模拟理解成一个思维模型。 毕竟这是一篇blog，所以对 R₀ 指数型回报的推到从简，可以点击这个视频详细了解可视化的推导过程以及提到的一些延展阅读12。 同时，这篇文章发布的时候，全世界已经经历了3年有余的"疫情"*。所以一些基础的概念：核酸，疫苗，等概念不做详细介绍。 而且我本身不是医学专业人士，更多是作为一个普通人在掌握高中数学知识的情况下，做一些基础的推论。欢迎大家指正。

*疫情 这个词语在这篇文章的语境里，超出病毒本身，而且包涵应对病毒的一系列政策引起的社会问题，这里主要讨论“核酸”和“疫苗”的投入和使用。

模拟疫情的解决的收益：核酸检测&疫苗接种

在2019-2022年这个三年中，大多数人都有过接受“核酸测试“或者”接种疫苗“的经验。分别对应的，就是解决上面函数中的 n₀ 和 R₀ 两个变量。进一步说，就是:

  • 通过【核酸🧪】测试不断发现，监测 n 然后配合医疗的措施和自然康复的过程，当然还有死亡。
  • 通过【疫苗💉】接种来降低 R₀*，因为大规模人群获得了免疫，阻止或者减慢了病毒的传播，从而导致 n 的增速减慢。

*\(R_{actual}\): 通过疫苗，提高人群的接种率，形成免疫屏障，其实是把实际的 R₀ 减小，导致最后的 n 的增速减慢。这样，加入资料和康复，最后 n 的数值可以减小。

重要的假设

其实核酸本身不直接治疗传染病，更多是在发现阳性病例后，有针对的接受医疗资源，来减慢 n 的增速，减小对社会运行产生的损失。所以在这里，我们不给核酸检测和疫苗接种之后接受的医疗资源投入设定一个上线，来简化讨论，减少参数。

收益的宽泛定义

宽泛指在采取了以上两种公共医疗措施之后，直接的经济收益，以及避免了死亡，减少死亡，弥补的社会效率损失后的间接经济收益。

模拟大规模核酸🧪收益

这里我们借用一个计算机科学的术语 for 循环

计算机科学

for loop 中文翻译 for 循环 是计算机科学中语言的迭代陈述3， 可以近似的理解成在设置初始化后，满足一定的条件进行递增迭代的重复操作，直到满足循环的终止条件。

Example

比如我们要给10个人坐核酸测试，那么就可以简单的表达成下面语句： 

for i in [1, 2, 3, 4, ..., 10]:
    核酸测试i
    打印核酸测试i结果
这个程序会持续一直会打印核酸测试结果从 1 到 10。

从上面的例子可以看出，这种程序反应的思路很直观，也很直接，也就是在确定 [1, 2, 3, 4, ..., n] 之后重复的执行就可以了。自然而然，可以想到的，重复执行的资源很大程度上由递增迭代决定，也就是 n 的大小。

如果每次做核酸的发现阳性病人之后综合下来的收益是r，最后的：

\[R_t = n*r - I_t\]
  • \(I_t\): 核酸测试的先期投入（initial Investment of Test）
  • \(R_t\): 核酸测试的收益

结论

\(R_t = n*r - I_t\) 这个简单的函数可以告诉我们，做核酸的收益就是线性的回报。

模拟大规模接种疫苗💉收益

关于大规模接种疫苗 \(R_0\) 指数型的回报，我们简单的从其定义2出发, 尤其当 \(R_0 > 1\) 的时候，比如：

Example

当 \(R_0=2\)，就是1个人，传染给2个人，然后2个人各传染给2个人，这样第二轮传播之后就4个人，这就是指数型（exponential）增加。

img

R0 virus spreading simulation from Washington Post Source:Reference [1]

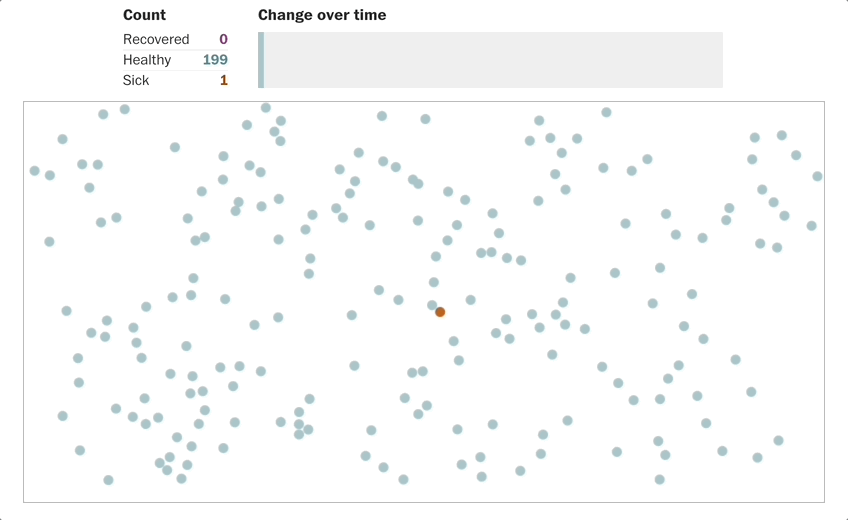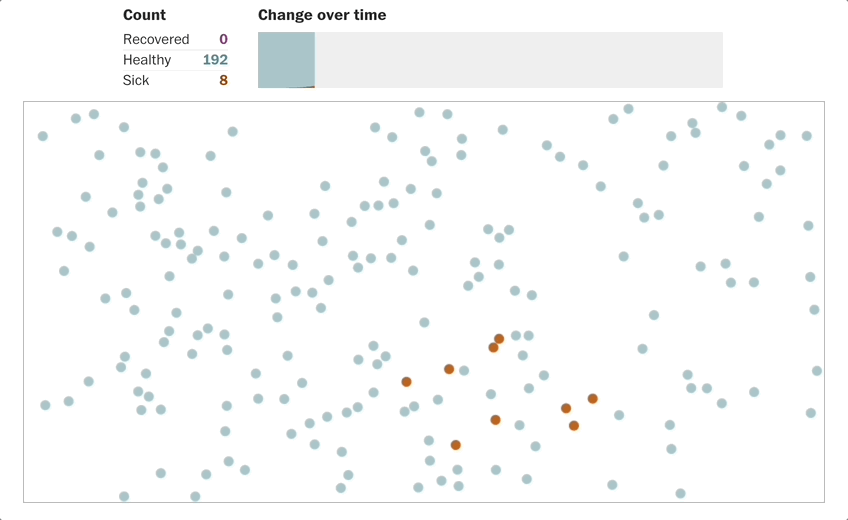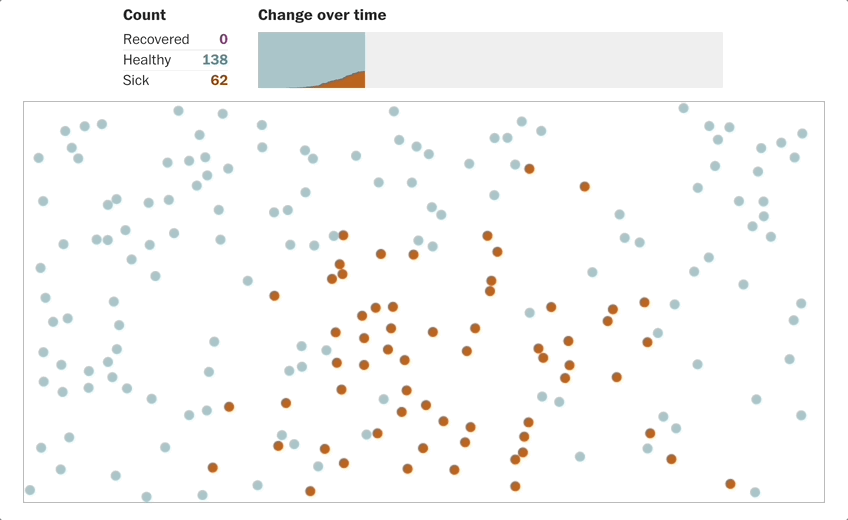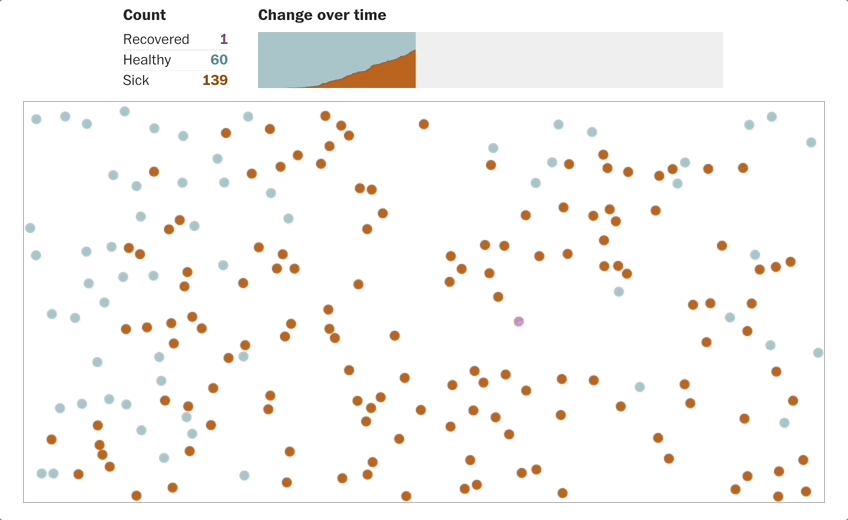
结论

那么如果我们能够通过疫苗，从\(R_0\)的角度解决，那么:

\[R_v = R_{0}^{f(n)} - I_v\]

esp when \(R_{0} > 1\)

  • \(I_v\): 疫苗研发的先期投入（initial Investment of Vaccination）
  • \(R_v\): 疫苗的收益
  • \(f(n)\): 宽泛的疫苗接种的函数作用于潜在的人群数n

收益曲线的绘制📈

  • 大规模核酸🧪：\(R_t = n*r - I_t\)
  • 大规模接种疫苗💉：\(R_v = R_{0}^{f(n)} - I_v\)

img

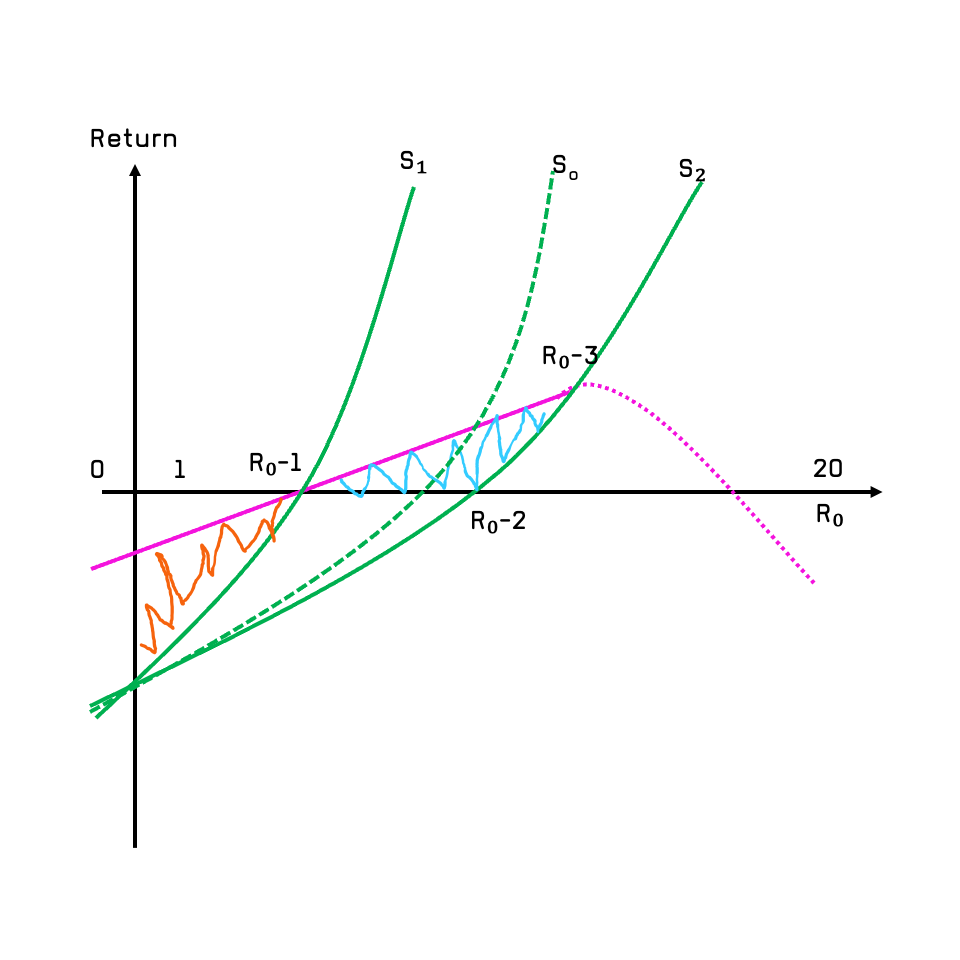
  • X：R₀值从0到20
  • Y：Return 收益
  • 紫色实线🟪: 核酸收益的线性曲线
  • 紫色虚线🟪: 核酸收益当 R₀ 到一个临界值的时候，核酸的收益曲线会快速下降

尤其当阳性病人数 n 的增速因为 R₀ 变得越来越大的时候，再做核酸就会变成负收益。

  • 绿色实线：疫苗接种收益的指数型曲线

Warning

其实疫苗接种收益的指数型曲线也是会遇到最终边际收益递减的情况，因为对应每种病毒，达到群体免疫的接种率门槛阈值时不一样的。 简单来说，传播力越弱的病毒接种率的门槛越低，总体接种人群数量越低，这样一来，再继续接种的收益就不明显了。

收益ROI的模拟: 核酸收益和疫苗收益的比较

S₁ 收益情况

S₁ 收益情况

在某个 R₀值 的时候，核酸和疫苗同时使用

那么两者比较的综合收益差 \(ΔR = R_v - R_t\) 就是： S₁绿色曲线下 X， Y轴的面积 减去 紫色实线下 X， Y轴的面积，因为都是负值，也就是橘色🟧阴影部分。

S₁ 收益情况结论

在S₁ 的情况下，核酸作为主要手段的收益 > 接种疫苗作为主要手段的收益 实际情况就是，疫苗的研发巨大的前期成本，已经时间上往往滞后与核酸测试技术的应用。由先天的临床研发上市周期决定。

S₂ 收益情况

S₂ 收益情况结论

当 R₀ 到一个临界值的时候，核酸的收益曲线会快速下降， 尤其当阳性病人数 n 的增速因为 R₀ 变得越来越大的时候，再做核酸就会变成负收益。也就是说在上图中，\(R_{0}3\) 之后，为保证综合收益的话，疫苗是必须作为主要解决手段的。综合收益差 \(ΔR > 0\)

img

S1 → S2: Sₒ收益情况

S1过渡到S2收益情况结论

当 \(R_{0}1\) < R₀ < \(R_{0}2\) 时，针对S₂疫苗为主的绿色实线，以核酸为主的解决手段收益还是比疫苗大的。也就是图中的蓝色🟦阴影面积。当然如果在 \(R_{0}1\) 之后能够早让疫苗为主的手段开始介入, 其实会有一条在S₁和S₂之间的最有\(S_{optimal}\)的疫苗接种收益曲线，这条曲线的综合收益差 \(ΔR = 0\) 也就是： 核酸的综合收益等于疫苗接种为主的综合收益，\(R_v = R_t\)

总结

  • 因为疫苗的先期投入成本巨大，和时间开发周期。疫情的先期，在 R₀值 导致的 n₀ 增速还在医疗资源承载能力范围之内的时候，核酸作为主导的解决疫情是正收益的方案。
  • 但是一旦疫苗研发完成，在短暂的窗口期，也就是医疗资源接近乃至超过承载上限的时候，那么核酸收益开始递减下降的时候就必须转为疫苗为主的解决方案才能保持正收益。也是上图中过了\(R_{0}3\)之后，和与之对应的时间窗口就是蓝色🟦阴影的区域。

Tip

实际情况就是需要我们对核酸检测人数, 阳性的数据采集，和实时追踪，尤其是运用比如 7天平均之类的数据平滑手段，检测 n 阳性新增人数的“增速”。一旦发现核酸的检测量已经无法跟上 n 阳性新增人数的“增速”，那这个时候已经宣告我们开始进入了“紫色虚线”的区域。这个时候你就需要疫苗为主的手段，而核酸采样就主要成为了检测的需要，而且是被动检测：人们感到不舒服了自己去做核酸，而不是主动式的筛查。

当然你也可以两个都不选择。

延展阅读/Further Reading

这篇文章的想法大概在2022年的4，5月份孕育。然后就在2022年11月21日，纽约市发表一篇文章3，是纽约市在推行疫苗接种Campaign上的收益计算，非常精细，可以具体算出 每1美元的花费，带来10.19美元的收益（降低感染率，死亡率，减少效率的损失，医疗资源的利用）。几乎10倍额收益，也就是指数型的回报。

最后

写这篇文章一是系统地整理自己的思路想法，同时也是给这段历史做一个从自己的经历和视角的注脚。撇开结论，大家也可以尝试下运用这种思路模拟实际的问题，为生活工作中的决策作出一定的参考。而不是模糊的计算或者gut feeling。

最后，再次感谢你投资宝贵的几分钟阅读到这里。

License

© CC BY-NC 4.0，转载引用请注明作者Hong(@hongwuxyz )和出处

  1. https://www.facebook.com/washpostvisuals (2020). Why outbreaks like coronavirus spread exponentially, and how to ‘flatten the curve’. [online] Washington Post. Available at: https://www.washingtonpost.com/graphics/2020/world/corona-simulator/ [Accessed 17 Dec. 2022]. ↩

  2. Meltingasphalt.com. (2022). Outbreak. [online] Available at: https://meltingasphalt.com/interactive/outbreak/[Accessed 17 Dec. 2022]. ↩↩

  3. Linear time: O(n) Plot, Access on Sun, Dec 4, 2022 9:47 ↩↩

  4. News-Medical (2020). What is R0? [online] News-Medical.net. Available at: https://www.news-medical.net/health/What-is-R0.aspx [Accessed 16 Dec. 2022]. ↩

  5. Sah, P., Vilches, T.N., Moghadas, S.M., Pandey, A., Gondi, S., Schneider, E.C., Singer, J., Chokshi, D.A. and Galvani, A.P. (2022). Return on Investment of the COVID-19 Vaccination Campaign in New York City. JAMA Network Open, [online] 5(11), p.e2243127. doi:10.1001/jamanetworkopen.2022.43127. ↩

Last update: December 22, 2022